Abstract

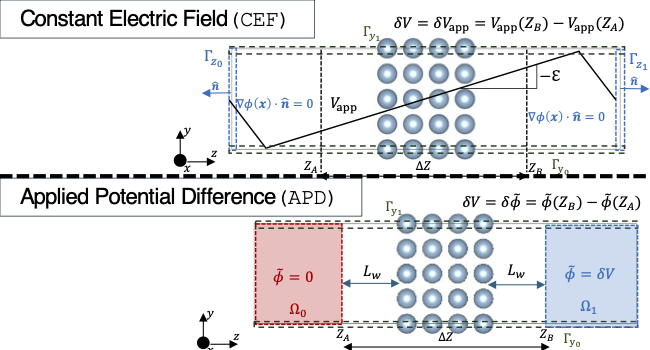
Accurate ab initio modeling of surfaces and interfaces, especially under an applied external potential bias, is important for describing and characterizing various phenomena that occur in electronic, catalytic, and energy storage devices. Leveraging the ability of real-space density functional theory (DFT) codes to accommodate generic boundary conditions, we introduce two methods for applying an external potential bias that can be suitable for modeling surfaces and interfaces. In the first method, an external constant electric field is applied by modifying the DFT Hamiltonian via the introduction of an auxiliary linear potential while solving the electrostatic potential arising in DFT using a Poisson equation with zero-Neumann boundary conditions. The second method directly enforces the desired external potential bias by imposing constraints on the electrostatic potential, thereby naturally mimicking experimental conditions. We describe the underlying DFT governing equations for the two setups within the real-space formalism employing finite-element discretization. First, we validate the constant electric field setup within real-space finite-element DFT (DFT-FE) with an equivalent approach using plane-wave DFT (i.e., using periodic boundary conditions) on three representative benchmark systems, namely, La-terminated Li₇La₃Zr₂O₁₂, GaAs (111), and Al FCC (111) slabs. Subsequently, we present a comprehensive evaluation of the two setups in terms of the average ground-state properties, such as surface and adsorption energies. Also, we present an approach to constrain the electrostatic potential over a localised region, which is non-trivial to implement in periodic DFT codes. The methods developed in our work provide an attractive alternative to plane-wave DFT approaches in applying external potential bias that usually suffer from the periodic boundary conditions restrictions and poor scalability on parallel computing architectures. Our framework offers a robust approach for investigating surfaces and interfaces without any underlying assumptions or correction schemes while allowing for simulations of larger length scales than possible with plane-wave DFT.